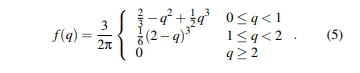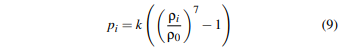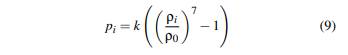이승민의 개발 블로그

SPH 탄생 배경

SPH의 탄생 배경은 SPH(Smoothed Particle Hydrodynamics)의 시초로 꼽히는 논문( Gingold & Monaghan 1977)에 잘 나와있습니다.

SPH는 1977년경 천문학 및 우주론 분야에서 처음 제안되었습니다.

당시 사용되던 오일러 방식(Eulerian)의 격자 기반 수치 해석 기법은, 고정된 격자(공간의 한 지점)를 기준으로 유체의 물리량 변화를 관찰하는 방식인데, 3차원 문제의 경우 격자 밀도가 급격히 증가하여 계산량이 기하급수적으로 늘어나 시뮬레이션하기 어려웠습니다.

이에 반해, 라그랑지안 방식(Lagrangian)은 유체를 구성하는 개별 입자 혹은 물질 덩어리를 따라가며 그 변화를 추적하는 방식으로, 자유 표면이나 큰 변형을 자연스럽게 처리할 수 있으면서 계산량을 줄일 수 있다는 장점이 있었습니다.

따라서, SPH는 계산 효율성을 크게 개선하고 복잡한 천체 물리 문제를 다루기 위해 이 라그랑지안 방식을 도입한 것입니다

그러면 Smoothing 함수가 무엇인가?

여기서의 스무딩 함수는 SPH에서는 각 입자가 고유의 질량, 밀도, 속도 등의 값을 갖고 있지만, 해당 값들이 하나의 점에 국한되지 않고, "주변 영역에 걸쳐 영향을 미치도록" 하기위해서 Smoothing 함수 정의하여 사용한다.

이 Smoothing 함수를 Kernel(커널) 함수라고 부르고, 이 함수는 보통 입자 사이의 거리와 Smoothing(평활화) 반경(h)에 따라서 가중치를 부여하고, 하나의 입자에 의한 물리량을 주변으로 "환산"시켜 마치 블러 효과를 주듯이, 마치 하나의 점의 영향력을 표현하자면, 하나의 점이 주변으로 스무딩되듯 부드럽게 연결한다.

위 사진은 커널 함수의 원리에 대한 사진이다. 한 입자에서 이웃 입자 사이의 거리와 평활화 반경(h) 매개변수로 kernel 입자에 전달해주게 되면, 얼마만큼의 가중치가 발생하는지를 알수있다.

여러 SPH Kernel Function 소개 : https://interactivecomputergraphics.github.io/physics-simulation/examples/sph_kernel.html

그렇다면 이 커널 함수의 결과를 어디에 사용하는가?

직전에 말했듯, 커널 함수를 통해서 한 입자와 다른 입자 사이의 거리와 평활화 반경을 통해서 얼마만큼의 영향력이 발생하는지를 알수있다고 했다.

그렇다면 평활화 반경을 통해 한 입자에서 평활화 반경 내에 있는 모든 입자들까지의 영향력을 알아낼수있다.

즉, 한 입자에서 평활화 반경 내에 존재하는 입자들과의 영향력의 총합을 통해, 해당 입자의 물리적 특성을 근사할수있다.

그렇게 해서 근사해낸 영향력으로 한 입자의 밀도를 구하고, 밀도로 압력을 구하고, 압력으로 힘을 구해서, 해당 입자가 다음 타임 스텝에 어느 방향으로 움직여야하는지를 근사해, 다음 위치를 계산하는 것이다.

그럼 먼저 사용할 커널 함수 방정식을 세운다.

평활화 반경(h)와 입자 사이의 거리(x)의 차에 세제곱(음수가 될수있으니 미리 0이상으로 설정)을 하면, 왼쪽 사진의 커널 그래프 모습과 비슷하게 오른쪽과 같이 나온다.

그런데 이 식을 그대로 쓰면안되고, 위 식을 통해서 나오는 값은 영향력 분포 형태를 정의하는것이다.

이걸 단위부피당 값으로 표현해서, 전체 부피를 1로 만들어야하기때문에 해당 위치에서의 부피로 나눠줘야한다.

그래서 위 적분식의 결과를 통해서 오른쪽의 식으로 부피를 구한다음 이걸로 나눠준 결과를 최종 영향력으로 사용하면된다.

이렇게 커널 함수를 설정하고, 이 결과 값을 가중치로 사용한다.

위는 입자를 64 x 64로 배치한 모습이다.

그렇다면 일반적으로 이 상황에서 "한 입자"에서 "평활화 반경 내의 밀도"는 어떻게 측정되어야할까?

모든 입자들이 동일한 간격으로 배치되어있으니, 반경 내에 입자들의 간격이 동일하다면, 입자 배치의 중심에서 평활화 반경을 증가시키거나 줄였을때, 측정되는 밀도는 항상 동일할것이다.

왼쪽은 평활화 반경이 1일때이고, 오른쪽은 3일때 측정한것인데, 수치가 비슷하지만 오차가 발생하는 이유는 부동소수점 연산때문에 그렇다.

위처럼 특정 평활화 반경에서 그 주변 입자의 몇몇 입자들과 밀도를 비교해서 거의 같으면된다

밀도 구하기

어떤 입자의 물리량을 다른 입자들과의 연관성을 통해서 알고싶을때 위 보간식을 사용해서 계산할수있다.

위 식은 위치 x에서의 물리량 A(x) 는 주변 입자 i 들의 물리량 A_i에 각 입자의 크기(부피)와 위치 x에 대한 영향력(커널 함수)를 곱한 값들을 모두 더해서 얻어진다. 라는 의미이다.

그랬을때, A_i가 밀도라고 하면, 이미 밀도로 나눠주기때문에 상쇄되어 사라지게된다.

그럼 최종적으로 밀도를 구하는 식은 위와 같다.

출처

https://www.researchgate.net/figure/The-principle-of-the-SPH-kernel-function-modified-from-90_fig6_334481027

https://www.youtube.com/watch?v=rSKMYc1CQHE&t=287s&ab_channel=SebastianLague

https://interactivecomputergraphics.github.io/physics-simulation/examples/sph_kernel.html

https://matthias-research.github.io/pages/publications/sca03.pdf

동작 과정

1. 파티클 해시 계산

파티클의 위치값과 셀크기로 해당 파티클의 해시 값 계산

 Particle p = Particles[index];

    // 파티클 위치 p.position 을 그리드 최소 바운더리 위치를 기준으로 상대 위치로 변환
    float3 relativePos = p.position - minBounds;

    // 상대 위치를 셀 크기로 나누어, 각 축별로 몇 번째 셀에 해당하는지 실수 값으로 계산
    float3 normalizedPos = relativePos / cellSize;

    // floor 연산으로 소수점을 버려 정수 인덱스를 얻음 (이때 음수 인덱스 가능성 있음)
    int3 cellID = int3(floor(normalizedPos));

    uint hashValue = uint(cellID.x) +
        uint(cellID.y) * gridDimX +
        uint(cellID.z) * gridDimX * gridDimY;

입력 : 파티클 버퍼

struct Particle {
		XMFLOAT3 position = XMFLOAT3(0.0f, 0.0f, 0.0f);
		float radius = 0.0f;
		XMFLOAT3 velocity = XMFLOAT3(0.0f, 0.0f, 0.0f);
		float life = -1.0f;
		XMFLOAT3 color = XMFLOAT3(1.0f, 1.0f, 1.0f);
		float density = 0.0f;
		XMFLOAT3 force = XMFLOAT3(0.0f, 0.0f, 0.0f);
		float pressure = 0.0f;
	};

출력 : 파티클 해시 버퍼

struct ParticleHash
	{
		UINT particleID = 0; // 원래 파티클 인덱스
		UINT hashValue = 0;  // 계산된 해시 값
		UINT flag = 0; // 그룹 시작 플래그
	};

2. 해시 값 기준 정렬

BitonicSort로 해시 값을 기준으로 오름차순으로 정렬 - Bitonic Sort 사용.

입력: ParticleHash

출력 : 정렬된 ParticleHash

3. 플래그 생성

정렬된 ParticleHash에서 i와 i - 1에서의 hashValue가 다르면 i 위치의 flag를 1로 설정

입력 : 정렬된 ParticleHash

출력 : 플래그 설정된 정렬된 ParticleHash

4. 플래그 스캔으로 그룹 생성

4-1. 지역스캔

스레드 그룹들끼리 공유 메모리를 이용해서 지역적으로 자기 위치 이전까지 몇개의 그룹이 존재하는지 측정

그룹 사이즈 - 1 위치의 값은 그 위치 이전에 지역적으로 존재하는 최대 그룹 수

그룹 사이즈 - 1 위치"까지"의 최대 그룹수는 그룹 사이즈 - 1 위치의 flag의 값이 1이면, 이전 최대 그룹 수에 1을 더해주면됨

4-2. 지역 스캔 결과로 나온 BlockSum들의 지역 스캔

4-1의 결과로 나온 그룹당 최대 그룹 수들의 모음을 가지고 4-1의 동작을 한번더 실행하면, 4-1의 각 그룹에 해당하는 그룹 Offset 값들( BlockSum )이 나오게 되고, 4-1의 지역 스캔결과와 4-2의 BlockSum을 연산해주면, 전체 정렬된 ParticleHash 의 각 객체에 해당하는 그룹들이 설정됨

입력 : 정렬된 ParticleHash

출력 : 전체 Scan

5. CompactCell 및 CellMap 설정

struct CompactCell
	{
		UINT hashValue = 0;
		UINT startIndex = 0;
		UINT endIndex = 0;
	};

4의 결과를 통해서, 각 그룹이 정렬된 ParticleHash에서 어느 범위에 해당하는지를 설정

스캔 결과의 현재 index 위치의 값이 그룹 값이 된다

5-1. 현재 index의 정렬된 ParticleHash의 flag가 1이라면, 현재 그룹의 startIndex에 해당함

5-2. 현재 그룹이 최대 그룹 개수 - 1이면, ParticleHash의 최대개수- 1이 endIndex가 되고, 그 외에는 CompactCell에서 현재 그룹 + 1인 다음 그룹의 startIndex가 endIndex가 된다.

5-3. 이후 uint로 이루어진 CellMap을 설정할건데, 현재 그룹의 해시값 위치의 CellMap값이 현재 그룹 값으로 설정된다.

이전에 CellMap의 각 값은 -1로 초기화된다.

6. 파티클 시스템

https://minsdevblog.tistory.com/28

참조

https://cg.informatik.uni-freiburg.de/publications/2014_EG_SPH_STAR.pdf

https://github.com/steampower33/LSMEngine

입자의 반지름(r) : 1.0

커널 크기(h) : 반지름 * 4

질량(m) : 0.5

압력 계수(pressureCoeff) : 5.0

기준 밀도(density0) : 1.0

점성 계수(viscosityCoeff) : 0.5

으로 설정해서 시뮬레이션을 진행했습니다.

위 과정을 진행하여 밀도, 압력을 구하고, 힘을 구해 속도와 위치를 업데이트합니다.

위 방정식으로 이전에 구한 밀도를 통해 압력을 구합니다.

그리고 위 방정식들을 통해서 각 입자의 힘을 구합니다.

커널 함수의 경우 위 식을 사용하는데, 현재 h^d를 f(q)에 나눠주게 되면 시뮬레이션이 불안정해져서 그 원인을 찾고있습니다.

입자개수 8192개를 렌더한 결과입니다.

참조

https://cg.informatik.uni-freiburg.de/publications/2014_EG_SPH_STAR.pdf

3차원으로 확장 가능한 경계 상자 정의

인접 입자 찾기 알고리즘

struct ParticleHash
{
    uint particleID; // 원래 파티클 인덱스
    uint hashValue;  // 계산된 해시 값
    uint flag;       // 그룹 Flag  
};

1. 위 구조체를 담는 배열을 생성하고, 아래와 같이 해시를 간단히 설정 -> 이후에 해시 생성 방식 변경

    // 파티클 위치 p.position 을 그리드 최소 바운더리 위치를 기준으로 상대 위치로 변환
    float3 relativePos = p.position - minBounds;

    // 상대 위치를 셀 크기로 나누어, 각 축별로 몇 번째 셀에 해당하는지 실수 값으로 계산
    float3 normalizedPos = relativePos / cellSize;

    // floor 연산으로 소수점을 버려 정수 인덱스를 얻음 (이때 음수 인덱스 가능성 있음)
    int3 cellID = int3(floor(normalizedPos));

    uint hashValue = uint(cellID.x) +
        uint(cellID.y) * gridDimX +
        uint(cellID.z) * gridDimX * gridDimY;

    ParticleHashesOutput[index].particleID = index;
    ParticleHashesOutput[index].hashValue = hashValue;
    ParticleHashesOutput[index].flag = 0;

2. 생성된 해시를 BitonicSort로 정렬하고(이후에 입자 개수가 많아질경우 Radix Sort 적용), 정렬된 해시 배열을 순회하면서, 이전 위치의 해시값과 지금 위치의 해시값이 다르면, 새로운 그룹으로 설정(flag = 1)

3. flag가 설정된 정렬된 해시 배열을 병렬 스캔 진행해서 전역 Prefix Sum 생성

효율적인 Belloch 병렬 스캔 알고리즘 적용(CUDA 예제 참고)

1. Pass 1 결과로 LocalScanSum이랑 PartialSum을 얻습니다.

2. Pass2에서는 PartialSum을 인풋으로, 결과를 blockOffsets를 얻습니다.

3. LocalScanSum이랑 BlockOffsets를 이용해서, 최종 PrefixSum을 얻습니다.

4. PrefixSum으로 그룹의 시작과 끝을 저장한 데이터를 출력합니다. 

참조

https://cg.informatik.uni-freiburg.de/publications/2014_EG_SPH_STAR.pdf

https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda

파티클 시스템 크게 두 단계로 구분

1. Compute Shader(이하 CS)를 이용한 SPH 연산
2. CS연산 결과를 그래픽스 파이프라인에서 렌더링 진행

1에서의 파티클 시스템은 현재 -1.0에서 1.0 사이의 랜덤한 위치에서, 7가지의 랜덤한 색상, 5.0의 생명주기를 갖습니다.

CS 내에서는 속도에 중력(-9.8) * dt 을 적용, 위치는 속도 * dt를 적용합니다. 생명주기는 -dt만큼을 적용합니다.

CS에서는 Ping-Pong 형식으로 버퍼를 설정해 사용합니다.

PIX를 통해서 버퍼간 데이터가 잘 전달되고 연산되는지를 확인합니다.

왼쪽은 맨처음 Dispatch에서의 Ping 버퍼, 오른쪽은 Pong 버퍼입니다. y값의 변화를 보실수있습니다.

다음은 그 다음 프레임에서의 Dispatch 입니다. 이전 프레임의 결과가 현재 프레임의 인풋과 동일합니다. 현재 프레임의 결과 또한 변경됨을 보이므로, 파이프라인 상에서는 문제가 없음을 확인하였습니다.

그래픽스 파이프라인에서의 파티클 데이터 렌더 -> 진행중

StructuredBuffer는 그래픽스 파이프라인에서도 사용가능하기에 SPH 결과 StructuredBuffer를 가져와 그래픽스 파이프라인에서 사용해 렌더합니다. 

vertex shader에서 파티클 정보를 geometry shader로 넘겨주고, 하나의 파티클 위치를 이용해 점 4개를 생성하고, 특정 위치를 바라보는 형식으로 구현합니다.

pixel shader에서는 얻은 정보들로 원하는 모양으로 파티클을 렌더한다.

Uniform Gird를 사용한 인접 입자 정렬 방식

1. 공간을 격자(Uniform Grid) 형태로 나누기
2. 2D 기준으로는 셀의 크기가 h인 격자의 셀로 (x,y)를 매핑한다고 했을때, cellX = x / h, cellY = y / h 가 셀의 인덱스에 해당한다
3. 셀 인덱스로부터 해시 값 만들기
4. 셀의 인덱스를 해싱해야하는데, 먼저 간단하게 hash = cellX + cellY * gridWidth로 설정한다.
5. 모든 입자들에 대해 (입자 ID, 해시 값) 쌍으로 묶은 것을 정렬
6. 입자 ID와 해시값 쌍을 넣은 자료구조를 새로 만들고, compute shader에서 Bitonic Sort를 사용해 해시 값 기준으로 정렬한다.
7. 정렬된 배열 순회하면서, 각 셀마다 존재하는 입자들의 범위를 미리 기록
8. 이웃 탐색 시 임의의 입자의 관심 범위 내의 입자들을 탐색
9. SPH에서 설정하는 커널 반경을 사용해 범위를 지정

해당 글은 SPH Fluids in Computer Graphics - https://cg.informatik.uni-freiburg.de/publications/2014_EG_SPH_STAR.pdf의 1장의 흐름에 따른 개념 정리 및 차후 본인의 진행 방향 설명 하는 글입니다.

해당 논문은 알고리즘이나 수학, 물리에 대한 깊은 지식을 기술한것이 아니라 이 당시(2014)에 좋은 성능을 끌어내던 기술들에 대한 내용을 기술하고있다.

지배 방정식을 가장 먼저 알아야한다. 입자가 존재하고, 이 입자 i는 고유한 질량(m_i)을 가지며, 밀도(ρ_i, rho), 압력(p_i), 부피(V_i), 위치(x_i), 속도(v_i) 등의 특성을 가진다. 결국 입자 시뮬레이션에서는 이 입자를 움직여야한다. 입자가 움직임, 즉, 위치 변화율(dx_i / dt = v_i)을 구해야하고, 위치 변화율은 그 입자의 속도(v_i)와 같다. 그러므로, 새로운 위치 = 현재 위치 + 속도 * dt와 같이 게산된다. 이것을 이류(Advection)이라고한다. 이류는 움직이는 유체와 함께 물질 또는 보존량이 이송되는 것을 의미한다.

다음으로 위치를 알기위한, 속도를 얻어야하는데, 이것을 운동량 방정식(Momentum Equation)인 Navier-Stokes를 이용한다. 이것의 의미는 입자 i의 속도 변화율(dv_i / dt), 즉 가속도(acceleration)는 여러 힘들의 합에 의해 결정된다. 이 방정식은 유체 동역학의 핵심인 나비에르-스토크스 방정식을 라그랑주 관점(Lagrangian perspective)에서 본것이다.(즉, 개별 입자를 따라가면서 보는 관점) 이 가속도를 계산해서(새로운 속도 = 현재 속도 + 가속도 *dt), 다음 시간 스텝의 속도를 얻는다.

라그랑주 관점에서의 나비에 스토크스 방정식의 각 항을 분석한다.

각 항은 가속도에 해당한다. 속도를 구하기 위해서 가속도를 알아야하기때문에 각 항은 가속도의 값을 가진다는 것을 알아야한다.

1. 압력 항
   유체 내의 압력 차이로 인해 발생하는 가속도이다. ∇p_i는 압력의 gradient로, 압력이 가장 급격하게 증가하는 방향과 크기를 나타낸다. 사실 압력 값 자체는 스칼라 값이지만, 스칼라의 gradient는 벡터(방향과 크기)이다. 유체는 압력이 높은 곳에서 낮은 곳으로 밀려나려는 경향이 있고, ∇p_i는 압력이 증가하는 방향을 가리키므로, 앞에 붙은 음수 부호(-)는 힘이 압력이 감소하는 방향, 즉 고압에서 저압방향으로 작용하게만든다. 1/p_i는 밀도가 높을수록 같은 압력 차이(gradient)에 대해 덜 민감하게 반응(덜 가속)함을 의미한다.(a = F/m)
2. 점성 항
   서로 다른 속도로 움직이는 입자들 사이의 마찰력(friction), 즉 점성으로 인한 가속도를 의미한다. ν(뉴, nu)는 동점성 계수(kinematic viscosity)로, 유체의 끈적이는 정도를 나타낸다.(물이 꿀보다 ν가 훨씬 작음) ∇²v_i는 속도의 라플라시안(Laplacian)으로, 주변 입자들과의 속도 차이를 측정하는 역할을 한다. 어떤 입자의 속도가 주변보다 훨씬 빠르거나 느리면 점성항이 커져서, 속도 차이를 줄이는 방향(즉, 주변 속도와 비슷해지도록)으로 힘이 작용한다. 즉, 속도를 부드럽게 퍼뜨리는 역할을 한다. 유체의 자연스러운 감쇠 효과(흐름이 점점 느려지는 것)을 만들고, 시뮬레이션의 수치적 안정성(stability)을 향상시키는 데 도움을 준다. 텍스트에서는 실제 물의 점성 계수( ν ≈ 10⁻⁶ m²/s)보다 더 큰 값을 SPH 안정성을 위해 사용하거나, 인공 점성(Artificial Viscosity, Mon92) 또는 XSPH(Mon89) 같은 대체 기법을 사용하기도 한다. (점성 “계수”임 즉, 스칼라값)
3. 기타 힘 항
   압력과 점성 외에 입자에 작용하는 다른 모든 외부 힘 또는 체적력(Body Force)로 인한 가속도이다. F_i ^ other 는 임자 i에 작용하는 외부 힘의 합이고, 이를 질량 m_i로 나눈 것이 가속도이다. ( 뉴턴의 제 2법칙, a = F/m) 가장 대표적인 것이 중력이다. 그 외에 사용자가 인위적으로 가하는 힘(예: 파도 생성), 표면 장력(surface tension, 때로는 별도 항으로 처리), 전자기력 등이 포함될 수 있다.

논문에서의 1.2 SPH절에서는 이전 지배 방정식을 실제로 입자 시스템에서 어떻게 계산하는지 알아본다. 수학적 도구와 근사 방법을 설명해준다. 핵심은 “이산적인 입자 정보로부터 연속적인 유체 정보(값과 그 미분)를 어떻게 보간할 것인가?” 이다. 논문에서는 SPH는 임의의 위치에 유체량을 보간하고, 유한한 수의 샘플 위치(인접 입자)로의 공간 미분을 근사하는데 사용된다고한다. 임의의 위치에 유체 물리량(밀도, 압력 등)과 공간적 미분(gradient, divergence, Laplacian)을 주변에 있는 유한한 개수의 인접 입자들의 정보를 이용하여 보간(interpolate)하고, 근사(approximate)하는 방법이다.

먼저 보간의 공식은 위와 같다. 임의의 입자 i에서의 물리량 A의 값(A_i)은 그 주변에 있는 모든 인접 입자 j 들의 물리량 값(A_j)에 가중치를 곱하여 합산함으로써 근사적으로 계산할수있다는 것이고, 가중치(W_ij)는 커널 함수라고하며, 이것이 SPH의 핵심이라고할수있다. 입자 i와 j 사이의 거리에 따라 가중치를 부여하는 함수이다. 가까울수록 큰 가중치, 멀수록 작은 가중치를 부여한다.

커널함수는 위와 같다. 이름처럼 함수이므로, 괄호안에 들어가는 q에 대해서 알면된다. ||x_i - x_j||는 입자 i와 j 사이의 거리이고, h는 스무딩 길이로 커널함수의 영향력을 미칠 반경을 결정하는 값이다. 즉, 임의의 입자에서 h 값 범위 내에 있는 입자들을 “인접 입자”로 간주할것이다. 그러기에 아주 중요하다. 그래서 입자 사이의 거리(r) / 스무딩 길이(h) 이므로, 정규화된 거리이다. 보통 f(q)를 r / h로 표현하고, 1 / h^d를 곱해주는 이유는 모든 방향에 대한 커널 함수의 적분 값이 1이 되도록 보장하는 역할을 해준다. 그래서 d의 값은 공간의 차원에 해당한다(2차원이면 2, 3차원이면 3).

그리고 커널함수의 종류는 다양한데 여기서는 3D SPH에서 흔히 사용되는 큐빅 스플라인 커널을 사용한것이다. 위 공식 처럼 q값의 범위에 따라 다르게 정의되는 구간별 함수이다. q가 2이상이면 값이 0이 된다.

그다음으로 중요한 위의 공간미분(Spatial Derivatives)이 있는데, 순서대로 gradient, divergence, laplacian 이다.

이전에 소개하지않는 것은 x_ij인데 이것은 입자 i와 j 간의 벡터 차이다.

논문의 1.3. Concept of an SPH-based Fluid Solver절에서는 이제 근사 방법에 대해서 알았으니, 실제 구현하기 위한 구조와 절차를 설명한다. SPH 기반 유체 솔버의 기본 구성 요소는 다음과 같다.

1. 이웃 탐색(Neighborhood search)는 각 입자 i에 대해서 주변 이웃 입자들을 효율적으로 찾는 과정이다. 한 입자에 대해서 다른 입자 모두를 비교하게되면, O(N^2)이 되어 너무 느리기 때문에 보통은 공간 분할 자료구조(Spatial access structure), 특히 균일 격자(Uniform Grid)를 사용해서 가속한다. 격자의 셀 크기는 보통 커널 함수의 영향 반경(ex: 2h)와 비슷하게 설정하여, 해당 셀과 인접 셀들만 탐색하면 되도록한다.
2. 압력 계산(Pressure computation)은 지배 방정식의 압력항에서 압력 gradient(∇p_i)를 구하기위해서, 먼저 각 입자의 압력 p_i를 알아내야한다. SPH에서는 보통 밀도 ρ_i로부터 압력 p_i를 계산한다.
3. 시간 적분(Time integration)은 계산된 힘(가속도)을 이용해 시간에 따라 입자의 속도와 위치를 업데이트한다.

압력 계산하는 방법으로 위의 상태 방정식을 이용한다(Equation of state, EOS) 밀도 ρ_i를 압력 p_i로 변환하는 함수로, SPH는 약간 압축 가능한 유체를 시뮬레이션하는 방식이기에 이 EOS는 밀도가 기준 밀도(ρ_0)에서 벗어날 때 얼마나 강하게 저항(압력 발생)하는지를 모델링한다. ρ_0는 유체의 기준 밀도이고, 유체가 안정 상태일 때 가지려는 목표 밀도이다. k는 강성 계수(Stiffness constant)로, 이 값이 클수록 밀도 변화에 대한 압력 반응이 커져서 유체가 더 비압축성처럼 행동하게된다. 하지만 k가 너무 크면 수치적 불안정성을 유발하므로, 매우 작은 시간 간격을 사용해야한다. 7은 상태 방정식의 지수인데 보통 7을 사용한다고함.

이후부터는 SPH의 여러 알고리즘에 대한 수도코드, Neighborhood 찾는 방법, EOS, Boundary Handling, Adaptive Time/Space Discretization, Multiphase Fluids, 입자 기반 인터페이스 표현 및 렌더링, 디테일 추가(거품, 스프레이, 공기방울 등), 향후 연구 방향에 대해 소개한다.

가장 먼저 Algorithm 1에 해당하는 SPH with state equation(SESPH)을 구현한다. 구현하기에 앞서 수도 코드에 대해 설명한다.

1. 먼저 어떤 입자에 대해서 이웃 입자들을 찾는다. 여기서는 앞서 언급한 Uniform Grid를 사용한다.
2. 어떤 입자의 밀도를 계산하는데, 이웃 입자들의 질량과 커널 가중치의 기여도의 합산으로 계산하고, 그 밀도를 이용해서 아래식으로 압력을 구한다.

   

3. 힘을 계산한다. 압력 gradient를 구해서 압력힘을 구하고, 속도 laplacian으로 점성힘을 구함. 이후에 파도 외부힘 구현할때, 이 항을 더 사용한다. 기본적으로 중력(g)를 설정한다. 이제 구한 힘을 다 더해 입자 i의 총 힘을 계산한다.
4. 마지막으로 시간 적분단계를 진행한다. 맨처음에 설명했듯이, 새로운 위치 = 현재 위치 + 새로운 속도 * dt이고, 새로운 속도 = 현재 속도 + 가속도 * dt이다. 최종적으로 구하고싶은 새로운 위치를 구해야하고, 현재는 a = F / m로 가속도를 구할수있다. 구한 가속도로 새로운 속도를 구하고, 새로운 속도로 새로운 위치를 구하면된다.

당장의 구현 방향은 다음과 같다. 앞으로 진행될 과정에 대해서는 최대한 작은 단위로 나눠서 세분화하도록한다.

1. 2D 파티클 시스템 구현 및 생명 주기를 가진 입자를 주기적으로 생성하고, 간단한 경계 충돌 테스트
   1. Compute Shader에서 구현
2. 2D 상에서 SESPH를 구현 및 입자 생성, 소멸, 간단한 경계 충돌 테스트
   1. 입자를 특정 위치에서 특정 속도로 생성. 인접 인자 확인은 Uniform Grid로 구현. 여전히 간단한 경계 충돌
3. 차원을 2D에서 3D로 확장하여 테스트

(사진을 클릭할시, 출처가 새탭으로 연결됩니다)

파도의 움직임을 4단계로 구분(shoaling -> propagating -> steepening -> breaking)되도록 구현합니다.

직육면체 박스안에서 각 면을 경계 조건으로 설정하고, 일정한 수면 높이 만큼을 파티클로 채워 초기 실행 화면으로 설정합니다.

파티클의 속도 변화를 직관적으로 관측하기위해서 파티클의 색이 변하는것으로 표현합니다. 기본적인 색은 RGB에서 (0, 0, 1)로 표현하고, 파티클의 속도가 증가함에 따라 G값을 증가시키고, B값을 감소시킵니다. 파티클의 속도의 감소 또한 반대로 작용합니다.

우선, 외부힘의 경우 시점의 오른쪽에 해당하는 면에서 가까운 특정 위치에서 수직으로 들어올리는 힘을 반복적으로 작용합니다. 이후 마우스를 이용해서 특정 위치에서 외부 힘이 적용되는 단계로 발전합니다.

이후 적용한 경계처리, 이웃 탐색, 충돌 감지 및 반응에서의 비용 등의 성능 측정을 위해, 직육면체 박스안에 고정된 하나의 물체를 설정하고, 물체의 크기와 파티클 개수에 따른 성능을 측정합니다.

#include <vector>
#include <queue>
using namespace std;

int solution(int n, vector<vector<int>> costs) {
    vector<vector<pair<int, int>>> graph(n);
    
    for (auto& edge : costs)
    {
        int u = edge[0], v = edge[1], cost = edge[2];
        graph[u].push_back({cost, v});
        graph[v].push_back({cost, u});
    }
    
    int totalCost = 0;
    vector<bool> visited(n, false);
    
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    
    visited[0] = true;
    for (auto& edge : graph[0])
    {
        pq.push(edge);
    }
    
    while (!pq.empty())
    {
        auto [cost, next] = pq.top();
        pq.pop();
        
        if (visited[next] == true)
            continue;
        
        visited[next] = true;
        totalCost += cost;
        
        for (auto& edge : graph[next])
        {            
            if (visited[edge.second] == false)
                pq.push(edge);
        }
    }
    
    return totalCost;
}

#include <string>
#include <vector>
#include <iostream>

using namespace std;

int visited[200];
int answer = 0;

void dfs(vector<vector<int>>& connects, int idx, int group)
{
    if (visited[idx] != 0)
    {
        return ;        
    }
    
    visited[idx] = group;
    for (auto& c : connects[idx])
    {
        if (visited[c] == 0)
            dfs(connects, c, group);
    }
}

int solution(int n, vector<vector<int>> computers) {
    
    vector<vector<int>> connects(n, vector<int>());
    
    for (int i = 0; i < n; i++)
    {
        // cout << i << " ";
        for (int j = 0; j < n; j++)
        {
            if (i == j)
                continue;
            if (computers[i][j] == 1)
            {
                connects[i].push_back(j);
                // cout << j << " ";
            }
        }
        // cout << endl;
    }
    
    for (int i = 0; i < n; i++)
    {
        visited[i] = 0;
    }
    
    for (int i = 0; i < n; i++)
    {
        if (visited[i] == 0)
        {
            answer++;
            dfs(connects, i, answer);
        }
    }
    
    return answer;
}

#include <string>
#include <vector>
#include <queue>
#include <iostream>

using namespace std;

vector<int> solution(vector<int> prices) {
    int n = prices.size();
    vector<int> answer(n, 0);
    
    // index, price, second
    queue<pair<pair<int, int>, int>> q;
    
    q.push({{0, prices[0]}, 0});
    for (int i = 1; i < n; i++)
    {
        int q_size = q.size();
        while (q_size > 0)
        {
            auto [index_price, second] = q.front();
            q.pop();
            
            int index = index_price.first;
            int price = index_price.second;
            second++;
            if (price <= prices[i])
            {
                q.push({{index, price}, second});
            }
            else
            {
                answer[index] = second;
            }
            q_size--;
        }
        
        q.push({{i, prices[i]}, 0});
    }
    
    while (!q.empty())
    {
        auto [index_price, second] = q.front();
        q.pop();
        
        int index = index_price.first;
        answer[index] = second;
    }
    
    return answer;
}